This article was written by Frank Kaputa & Mike Bannon
Gradients in air temperature can cause the direction of sound to bend and form acoustic shadows.
Sound travels faster in warmer air than in cold air. The following formula shows the speed of sound in air (c):
Equation 1
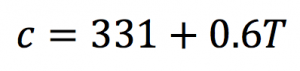
Here the speed of sound is in meters per second (m/s) and T is the temperature in degrees Celsius (°C).
Air is warmer at lower altitudes and decreases linearly with altitude. The equation that fits this general statement is1:
Equation 2
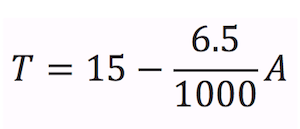
Here the temperature is in degrees Celsius and is the altitude in meters. This tells us that at sea level (altitude of 0) the air temperature is 15°C and that for every 1000m in altitude gained, the temperature drops 6.5°C. Obviously, this is a very general equation – we know that the air temperature at sea level is not always 15°C, and that weather and atmospheric conditions can drastically change things. We can use the general form of this equation for our experiment because it represents a linear temperature change as the altitude changes. A more general form of this equation is as follows:
Equation 3
Here is the temperature at our starting or reference point, which may or may not be sea level. represents a constant value that indicates the rate of the temperature change as the altitude changes.
A phenomenon known as temperature inversion is when the air temperature increases as altitude increases. This can occur over a cool body of water or due to weather conditions. In this case, the constant is a negative value.
Digging Deeper
If we combine equations 1 and 3, we can write a formula to determine the speed of sound at a given altitude:
Which reduces to
Since 0.6k is a constant, we can call it k' and simply our equation:
Equation 4
As sound moves through air at varying temperatures as described above, the wave front distorts. As it distorts, it is claimed that the sound bends in the direction of the distortion. See the figure below.
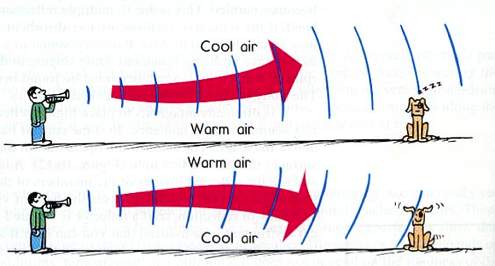
In the first case the sound “bends” upwards and it is theorized that the dog may not hear the sound as it is directed up and away from him. In the second case, that of a temperature inversion, the sound is directed downwards and the dog will hear the sound even better than if there was no temperature variation.
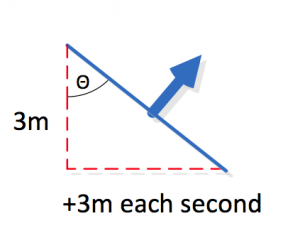
Let us look at the wave front from the first case a little more closely. To keep things simple, let us have our wave emanate vertically, as from a wall, rather than from a point. This keeps the math simple, both for the author and for the reader. The bottom of the wave front, in warmer air, moves faster than the top of the wave front. See diagram below.
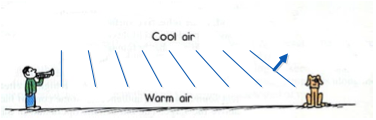
If in this example, if we make the top of the wave front 3 meters higher than the bottom of it, and declare a 5°C temperature difference in those 3 meters, than every second the bottom of the wave is traveling another 3 meters further than the top (see Equation 4). We can see that the angle of the wave front continues to change as the wave travels. If we look at the angle Θ as depicted below, we know it starts out at 0°, and gets larger each second the sound travels. Using the numbers from the example, the bottom of the triangle grows 3 meters each second.
If we want to write an equation for Θ, it is:
Θ = tan-1t
where t is the number of seconds. After several seconds, Θ approaches 90°, or a horizontal line.
What some have written is that the sound level will be higher, or louder, in the direction of the arrow. Some have also written that in this case the sound will “lift off” the ground and create an acoustic shadow, an area where the sound is not heard. Is this accurate? Perhaps an experiment can help us determine that.
Procedure for an Experiment
So how can we test to see if this theory is accurate? We can setup a computer with a speaker and generate sound at a certain frequency, and at a distance from that we can use another computer set up with microphones to listen for that frequency. If we setup the microphones at different heights (altitudes), we can see if the sound pressure level varies according to the model above. Additionally we can measure the temperatures at each of the microphone heights to get a better understanding of the temperature gradient.
To get a more exaggerated temperature gradient, the experiment can be done over an asphalt parking lot on a hot, sunny summer day. This will provide extremely hot temperatures near the parking lot surface and the air temperature will cool dramatically above it.
To exaggerate a temperature inversion, the experiment can be done over a frozen lake or pond on a warm spring day. This will provide cold temperatures (0°C) near the ice, but the air temperature above it will be significantly warmer.
Conclusion
It has been written that sound bends due to differences in air temperature and acoustic shadows can form. Not much empirical data seems to exist to support this. Perhaps the experiment described above can provide data to support this. I hope that we will be able to do this experiment and share that data.
1 http://usatoday30.usatoday.com/weather/wstdatmo.htm, from AERODYNAMICS FOR NAVAL AVIATORS BY H. H. HURT, JR. UNIVERSITY OF SOUTHERN CALIFORNIA 1965.
